Ecuacion Polar (Graficacion) r=Sen(x)

Graficacion de cordenadas polares

Área y Longitud de Arco de una coordenada polar.

Tipos de Ecuaciones Polares

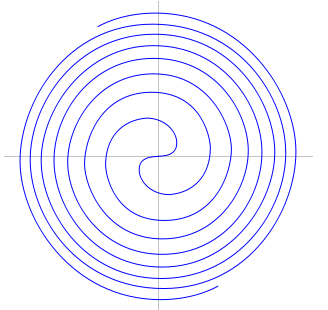
 Espiral de Euler.

Donde:

L          :           Longitud desde el origen a los puntos indicados, (m)

R         :           Radios en los puntos indicados, (m)

A         :           Parámetro de la clotoide, (m)

Cardioide

 ecuación polar es: ρ=a(1+cos θ),

(x^2+y^2-2ax)^2 =4a^2(x^2+y^2)

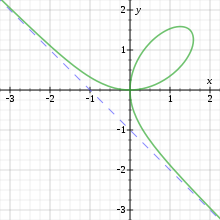
Bifolium 

ecuación polar es (x^2+y^2)^2 =(ax+by)x^2

Espiral Logarítmica

ecuación polar es r=ce*Θ

Θ=log (r/a)

Θ=1/h log (r/c)

Rosas

                                Estas ecuaciones polares son rosas de varios pétalos.

                               El número de pétalos de la rosa depende de "n".

Espiral de Fermat

Ecuacion Polar  es r=a*(Θ)1/2

Folium de Descartes 

Ecuación polar es : x^3 +y ^3-3a xy=0

Espiral de Arquimides

Ecuación polar es : r=a+bΘ

Lemniscata 

r^2= 2n^2 cos 2Θ

Las rosas de Nathersan

Las rosas de Nathersan

Distancia entre dos puntos.

                                          P(1,0,0) Q (0,2,0) R (0,0,3)      Triangulo Escaleno  

                                            P (2, 1,5) Q (-1, 3,4) R (3, 0,6)      Triangulo Escaleno  

                                                             P(0,-2,0) Q (4,1,-2) R (5,3,1)      Triangulo Escaleno  

  

Bosqueje:

                                                             b (y, z) = y² + 5z²

                                                                          a (y, z) =  4y² - z² - 4

                                                                    a: x² - z² = 4

                                                                   a: 9x² - 16y² = 16

                                                                            z² - x² = 0  

Use una computadora con software de graficación tridimensional para dibujar la superficie.

-4x^2-y^2+z^2=1

-4x^2-y^2+z^2=0

x^2-y^2-z=0

x^2-6x+4y^2-z=0

Epitrocoide

Área de un triangulo con vértices

encuentre el área del triangulo con vértices P(1,4,6) Q(-2,5,-1) R(1,-1,1)

a = RP=(x1-x2 , y1-y2 , z1-z2)
           =(1-1 , 4-(-1) , 6-1)
           =(0,5,5)

b = RQ=(-2-1 , 5-(-1) , -1-1)
            =(-3,6,-2)

         i   j   k           5  5         0  5          0  5
axb= 0  5  5     = i  6 -2   -j  -3 -2  +k  -3  6
        -3  6 -2

= i{(5)(-2) - (6)(5)} -j{(0)(-2) - (-3)(5)} +k {(0)(6) - (-3)(5)}

=i(-10-30) - 15j + 15k = (-40,-15,15) = n

ǀaǀ = √a1²+a2²+a3²

ǀaxbǀ = √(-40)²+(-15)²+(15)²

ǀaxbǀ = 5√82

= √25√82 = √25.82 = √2050

como se necesita la mitad para el triangulo

APRQ=5/2 √82 = √2050/2

El angulo entre 2 vectores

a•b = ǀaǀ ǀbǀ cos Ǿ

cos Ǿ = (a•b / ǀaǀ ǀbǀ)

Ǿ = cos -1(a•b / ǀaǀ ǀbǀ)


Ejemplo

a=(2,2,-1)         b=(5,-3,2)

ǀaǀ=√ 2²+ 2²+ (-1)²          ǀbǀ=√ 5²+ (-3)²+ (2)²

ǀaǀ =√9 = 3                      ǀbǀ=√25+9+4 

                                       ǀbǀ=√38

cos Ǿ = (a•b / ǀaǀ ǀbǀ) = (2)(5)+(2)(-3)+(-1)(2) / 3√38 = 10-6-2/3√38 = 2 / 3√38

Ǿ= cos-1 (2 / 3√38) = 84º

Ortogonalidad

a y b son ortogonales si y solo si a•b=0

Ejemplo 

2i+2j-k            y      5i-4j+2k

(2,2,-1) • (5,-4,2) =  10-8-2 = 0  son ortogonales

EjemplO

a= (1,2,3)

ǀaǀ=√1²+ 2²+ 3²  =√14


cos α = 1/ √14           α= COS-1 (1/√14) = 74.49 = 74º

cos β = 2/ √14           β= COS-1 (2/√14) = 57.67 = 58º

cos γ = 1/ √14           γ= COS-1 (3/√14) = 36.69 = 37º

Ejercicios de distancia entre puntos

Dados los puntos P,Q,R
Determine

A)Distancia entre los puntos
B)Que tipo de triangulo forman

1.- P(1,0,0) Q(0,2,0) R(0,0,3)

Triangulo escaleno

PQ=√ (0-1)²+ (2-0)²+ (0-0)²

PQ=√1+4

PQ=√5

PR= √ (0-1)²+ (0-0)²+ (3-0)²

PR=√1+9

PR=√10

RQ=√ (0-0)²+ (0-2)²+ (3-0)²

RQ=√0+4+9

RQ=√13

2.- P(2,1,5) Q(-1,3,4) R(3,0,6)

Triangulo escaleno

PQ=√ (-1-2)²+ (3-1)²+ (4-5)²

PQ=√9+4+1

PQ=√14

PR= √ (3-2)²+ (0-1)²+ (6-5)²

PR=√1+1+1

PR=√3

RQ=√ (3+1)²+ (0-3)²+ (6-4)²

RQ=√16+9+4

RQ=√29

3.- P(0,-2,0) Q(4,1,-2) R(5,3,1)

Triangulo escaleno

PQ=√ (4-0)²+ (1+2)²+ (-2-0)²

PQ=√16+9+4

PQ=√29

PR= √ (5-0)²+ (3+2)²+ (1-0)²

PR=√25+25+1

PR=√51

RQ=√ (5-4)²+ (3-1)²+ (1+2)²

RQ=√1+4+9

RQ=√14

Wooton pag 281 1-35

9.-V=-3U        U=(3,-1,2) y W=(1,7,-6)
se tiene
V=-3U

3(3,-1,2) = (9,-3,6) entonces
V = (9,-3,6) - (1,7,-6)
V = (9-1 , -3-7 , 6+6)
V = (8,-10,12)

Capitulo 8 de Wooton

1.S(2,-1,5) , T(4,3,3)

a) V=(4-2,3-(-1),3-5) = (2,4,-2)

b) V=2i+4j-2k

c) ǀǀVǀǀ=√(2)²+(4)²+(-2)² = √4+16+4 = √24 = 2√6 = 4.8989

2.S(2,1,5), T(-2,2,-1)

a) V=(-3-2,2-1,-1-5) = (-5,1,-6)

b) V=-5i+j-6k

c) ǀǀVǀǀ=√(-5)²+(1)²+(-6)² = √25+1+36 = √62 =  7.8740

3.S(0,4,5), T(5,-1,0)

a) V=(5-0,-1-4,0-5) = (5,-5,-5)

b) V=-5i-5j-5k

c) ǀǀVǀǀ=√(-5)²+(-5)²+(-5)² = √25+25+25 = √75 =  8.66

4.S(3,0,-2), T(0,4,6)

a) V=(5-0,-1-4,0-5) = (5,-5,-5)

b) V=-5i-5j-5k

c) ǀǀVǀǀ=√(-5)²+(-5)²+(-5)² = √25+25+25 = √75 =  8.66

5.S(-3,-3,-3), T(3,3,3)

a) V=(3-(-3),3-(-3),3-(-3) = (6,6,6)

b) V=-6i+6j+6k

c) ǀǀVǀǀ=√(6)²+(6)²+(6)² = √36+36+36 = 6√3 =  10.392304

6.S(0,0,3), T(-3,0,0)

a) V=(-3-0,0-0,0-3) = (-3,0,-3)

b) V=-3i+0j-3k

c) ǀǀVǀǀ=√(-3)²+(0)²+(-3)² = √9+0+9 = √18 =  4.24

7.S(5,-1,0), T(0,0,-2)

a) V=(0-5,0-1,-2-0) = (-5,-1,-2)

b) V=-5i-j-2k

c) ǀǀVǀǀ=√(-5)²+(1)²+(-2)² = √25+49+1 = √30 =  5.477

8.S(8,-6,-2), T(5,1,-1)

a) V=(5-8,1-(-6),-1-(-2)) = (-3,7,1)

b) V=-3i+7j+1k

c) ǀǀVǀǀ=√(-3)²+(7)²+(1)² = √9+49+1 = √59 =  7.681

Capitulo 8 Wooton ejercicio 21 al 31

calcule la distancia que separa a los puntos
1.-S(1,1,2), T(2,3,4)

ST=√ (1)²+ (2)²+ (2)²

ST=√1+4+4

ST=√9

ST=3

2.-S(-1,1,3), T(0,-1,1)

ST=√ (-1)²+ (-2)²+ (-2)²

ST=√1+4+4

ST=√9

ST=3

3.-S(2,-1,5), T(0,2,-1)

ST=√ (-2)²+ (1)²+ (-6)²

ST=√4+1+36

ST=√41

ST=6.4031242371

Capitulo 12 Pag 784 Vectores y la geometria del espacio

(a) No se necesita poner un punto entre la C y el parentesis, con el parentesis solo significa que es una multplicacion
(c)En los valores absolutos solamente hay positivos y esto puede afectar en los valores si hay un negativo
(f)Es lo mismo que en la c, aparte se le esta agregando el punto

A• B= ǀAǀ•ǀBǀ•cos Ǿ
A=6
B=1/3
Ǿ=angulo entre AyB=π /4= 45º
AB=(6)(1/3) cos π/4=6*1/3*0.525321989
A•B=1.4142

Trazas

la intersección con los ejes coordenados implica hacer 2 variables cero de la ecuación, para obtener cada punto en los ejes coordenados. Las trazas serán con una variable
Intersección con los ejes

Trazar el plano 3x+4y+6z=12

para x=0, y=0                   para y=0,z=0                  para x=0, z=0
3(0)+4(0)+6z=12             3x+4(0)+6(0)=12           3(0)+4y+6(0)=12
z=12/6                              x=12/3                            y=12/4
z=2                                   x=4                                 y=3
P1(0,0,2)                          P2(4,0,0)                         P3(0,3,0)

Trazas
x=0                            y=0                             z=0
3(0)+4y+6z=12         3x+4(0)+6z=12          3x+4y+6(0)=12
4y+6z=12                  3x+6z=12                   3x+4y=12

Longitudes de los lados de los triangulos (Ejercicios)

Halle las longitudes de los lados del triangulo PQR. ¿Es un triangulo rectángulo?, ¿Es un triangulo isósceles?
1.-P(3,-2,-3) ,Q(7,0,1), R(1,2,1)

PQ=√ (7-3)²+ (0-(-2))²+ (1-(-3))²

PQ=√16+4+16

PQ=√36

PQ=6

PR=√ (1-3)²+ (2-(-2))²+ (1-(-3))²

PR=√4+16+16

PR=√36

PR=6

RQ=√ (1-7)²+ (2-0)²+ (1-1)²

RQ=√36+4+0

RQ=√40

RQ=6.32

 Triangulo Isósceles

2.-P(2,-1,0), Q(4,1,1), R(4,-5,4)

PQ=√ (4-2)²+ (1-(-1))²+ (1-0)²

PQ=√4+4+1

PQ=√9

PQ=3

PR=√ (4-2)²+ (-5-(-1))²+ (4-0)²

PR=√4+16+16

PR=√36

PR=6

RQ=√ (4-4)²+ (-5-1)²+ (4-1)²

RQ=√0+36+9

RQ=√45

RQ=6.70

Triangulo escaleno